suppressPackageStartupMessages({
    library(tidyverse)
    library(cowplot)
    library(ggrepel)
    library(pheatmap)
})
theme_set(theme_cowplot())
options(repr.plot.width=9,repr.plot.height=7)

PCA visualization in R

This guide illustrates how to visualize the results of a PCA analysis

There is a sister notebook to this one in Python here: PCA visualization in Python

Dataset

# iris dataset is part of R base
head(iris,5)

A data.frame: 5 × 5

	Sepal.Length	Sepal.Width	Petal.Length	Petal.Width	Species
	<dbl>	<dbl>	<dbl>	<dbl>	<fct>
1	5.1	3.5	1.4	0.2	setosa
2	4.9	3.0	1.4	0.2	setosa
3	4.7	3.2	1.3	0.2	setosa
4	4.6	3.1	1.5	0.2	setosa
5	5.0	3.6	1.4	0.2	setosa

Run a PCA decomposition

iris.data = select(iris, -Species)
pca_res = prcomp(iris.data)
dim(pca_res$x)

1. 150
2. 4

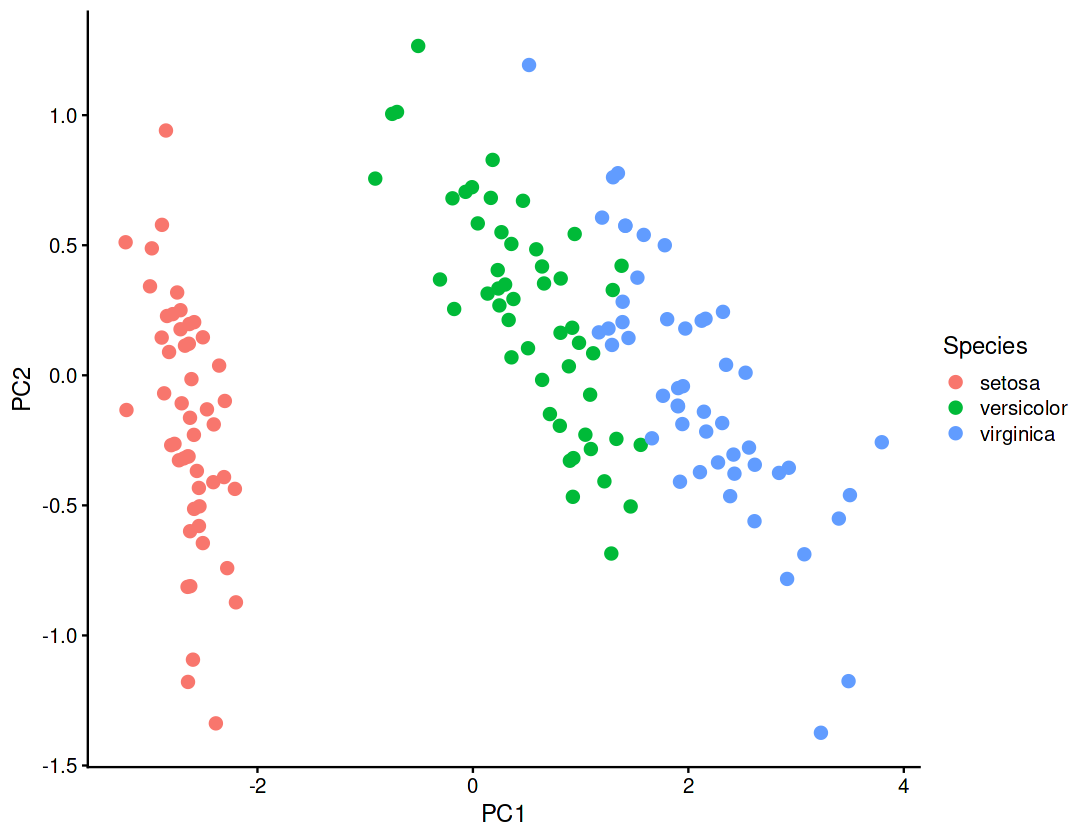
Scatter plot of observations

Observations are projected on the first 2 components

pca_res$x %>% 
bind_cols(select(iris, Species)) %>%
ggplot(aes(x=PC1, y=PC2, color=Species)) + geom_point(size=3)

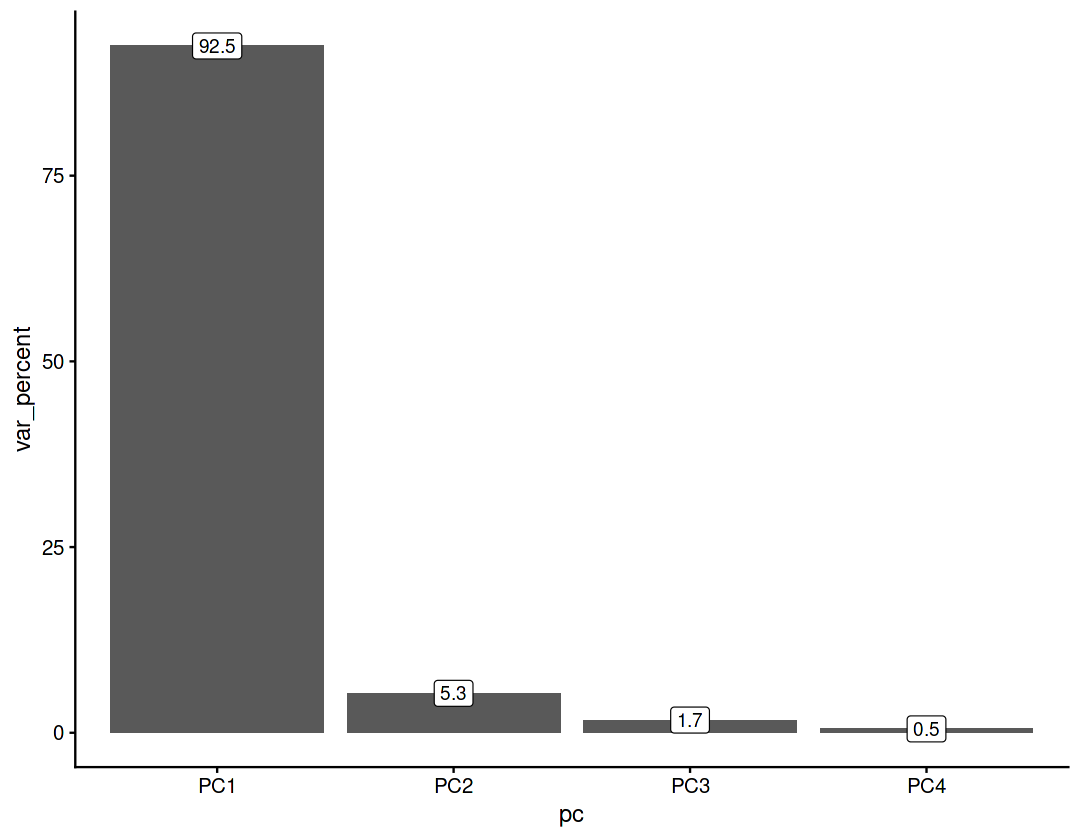
Explained variance (eigenvalues)

The amount of variance explained by each of the components

var = pca_res$sdev ** 2
var

1. 4.22824170603486
2. 0.242670747928634
3. 0.0782095000429193
4. 0.0238350929734494

tibble(var_percent=100*var/sum(var),pc=colnames(pca_res$x)) %>%
ggplot(aes(x=pc, y=var_percent)) +
geom_col() +
geom_label(aes(label=round(var_percent,1)))

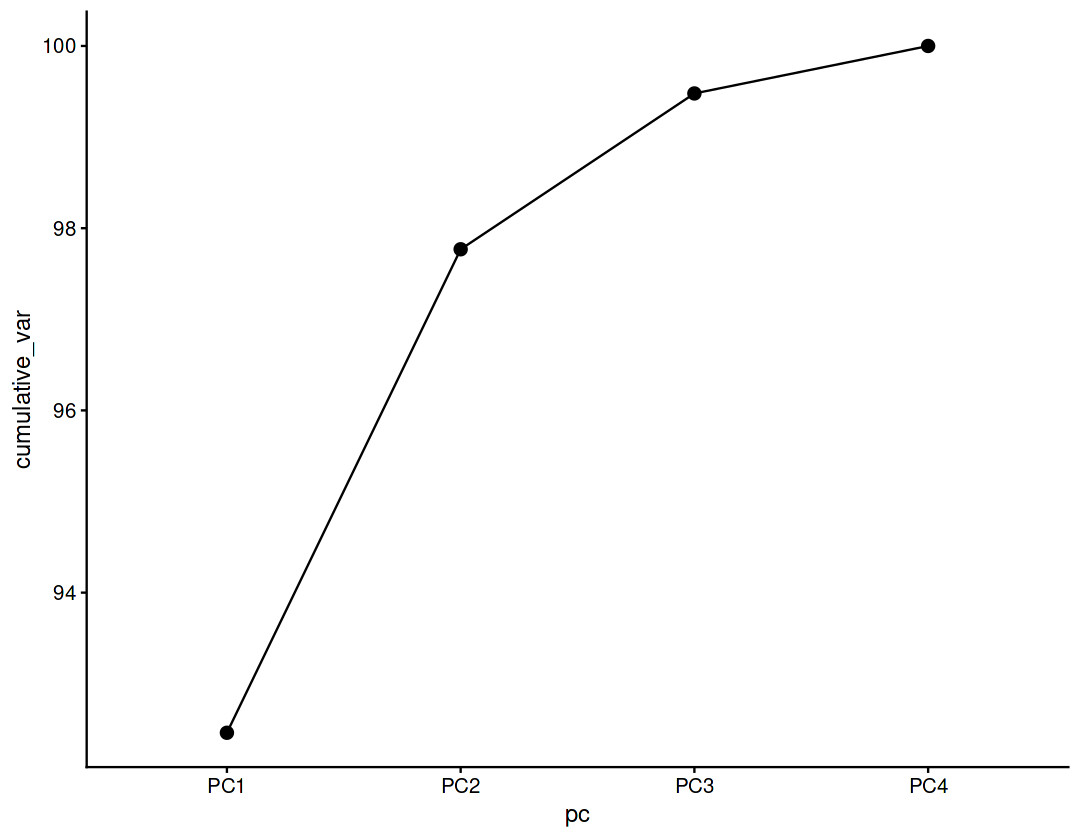
Cumulative variance

tibble(var_percent=100*var/sum(var),pc=colnames(pca_res$x)) %>%
mutate(cumulative_var=cumsum(var_percent)) %>%
ggplot(aes(x=pc, y=cumulative_var,group=1)) +
geom_point(size=3) +
geom_line()

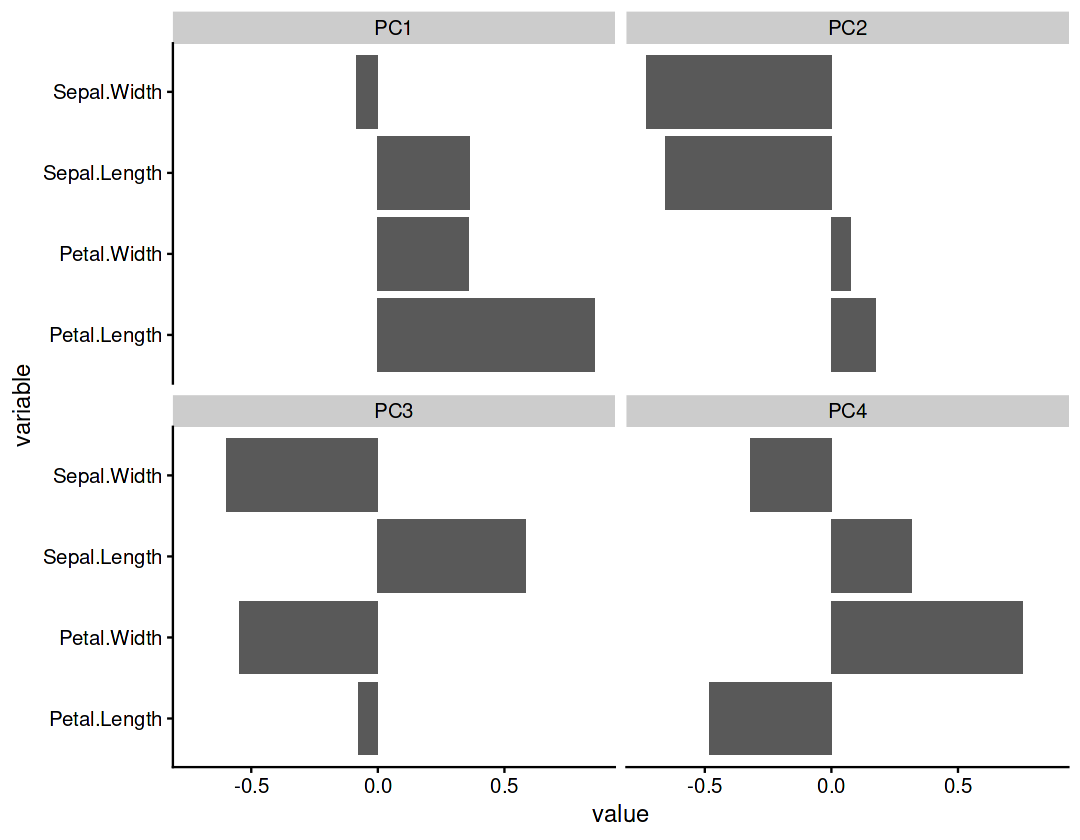
Component rotations (eigenvectors)

Principal axes in feature space, representing the directions of maximum variance in the data

pca_res$rotation

A matrix: 4 × 4 of type dbl

	PC1	PC2	PC3	PC4
Sepal.Length	0.36138659	-0.65658877	0.58202985	0.3154872
Sepal.Width	-0.08452251	-0.73016143	-0.59791083	-0.3197231
Petal.Length	0.85667061	0.17337266	-0.07623608	-0.4798390
Petal.Width	0.35828920	0.07548102	-0.54583143	0.7536574

pca_res$rotation %>% 
as.data.frame() %>%
rownames_to_column('variable') %>%
pivot_longer(names_to = 'pc', values_to = 'value', -variable) %>%
ggplot(aes(y=variable, x=value)) + geom_col() + facet_wrap(~pc)

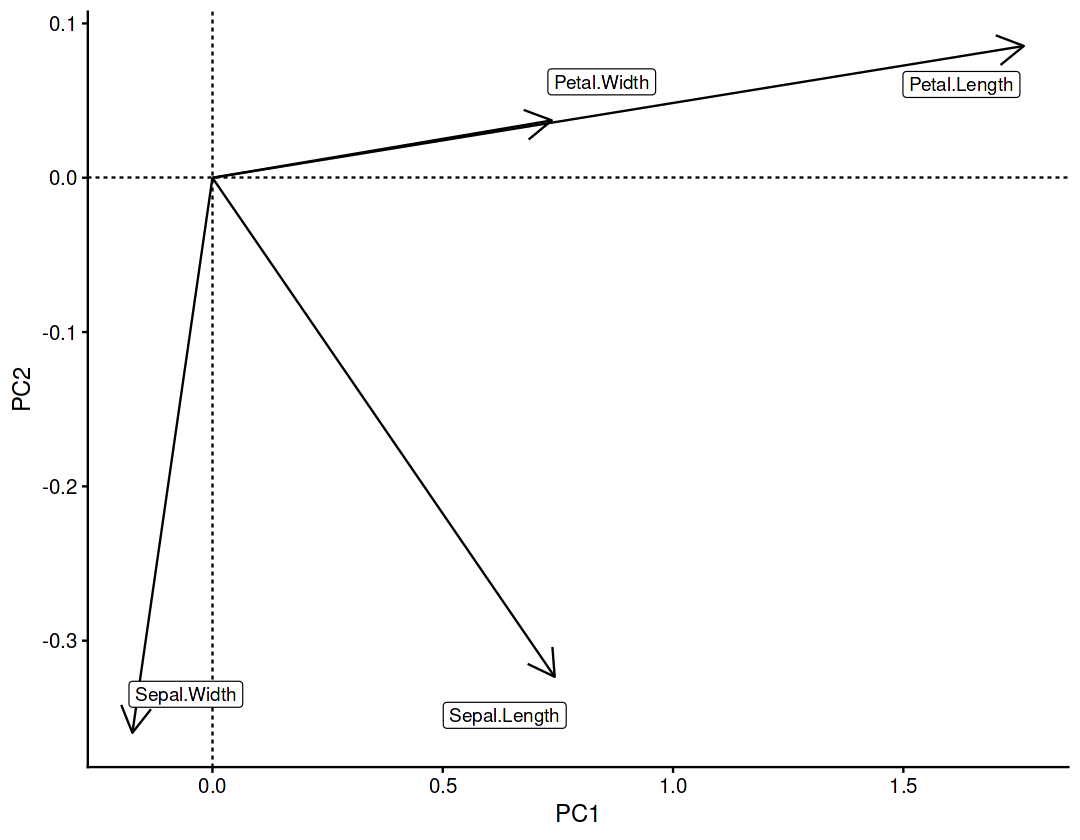
Component loadings

Eigenvectors scaled by the square root of the eigenvalues

var_cor = t(pca_res$rotation) * pca_res$sdev
var_cor

A matrix: 4 × 4 of type dbl

	Sepal.Length	Sepal.Width	Petal.Length	Petal.Width
PC1	0.74310800	-0.17380102	1.76154511	0.73673893
PC2	-0.32344628	-0.35968937	0.08540619	0.03718318
PC3	0.16277024	-0.16721151	-0.02132015	-0.15264701
PC4	0.04870686	-0.04936083	-0.07408051	0.11635429

m = max(abs(var_cor))
t(var_cor) %>% 
as.data.frame() %>% 
rownames_to_column('var') %>%
ggplot(aes(x=PC1, y=PC2)) + 
geom_segment(arrow=arrow(),aes(x=0,y=0,xend=PC1,yend=PC2)) +
geom_vline(xintercept=0, linetype=2) +
geom_hline(yintercept=0, linetype=2) +
geom_label_repel(aes(label=var),box.padding = 1, min.segment.length = Inf)

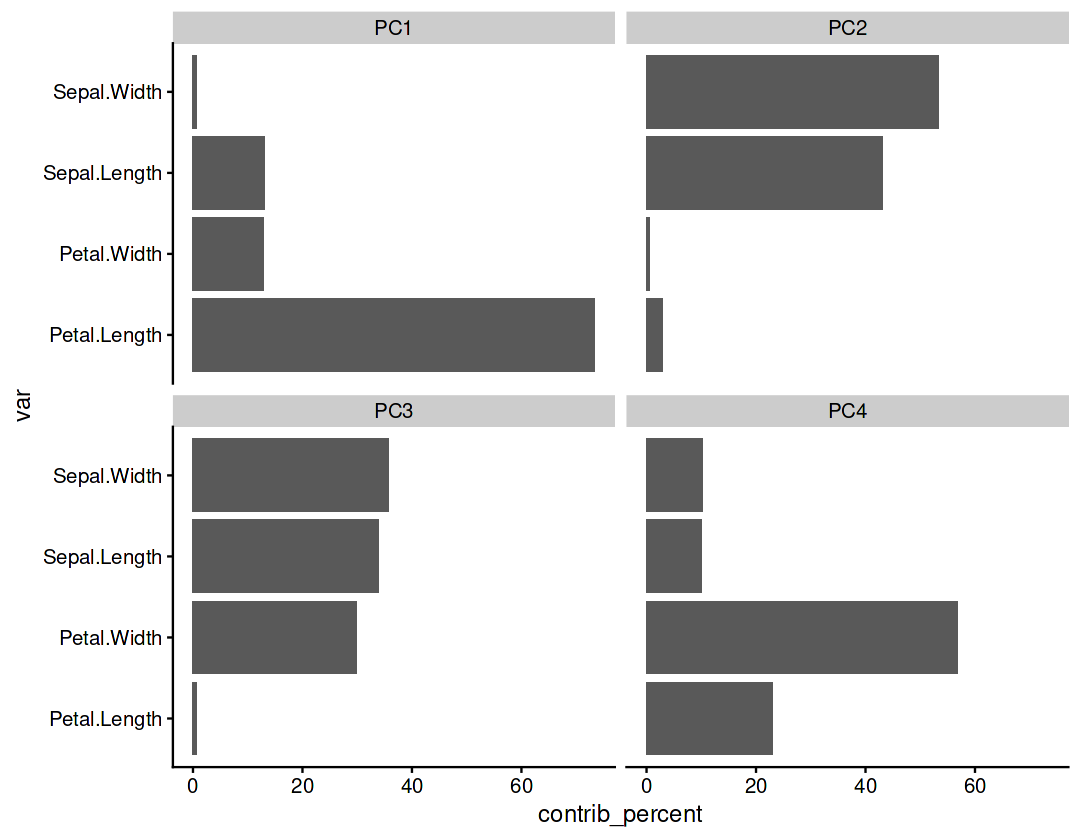
Component contributions

Measures the contribution of the variables to each component

var_cos2 = var_cor ** 2
var_contrib = (100 * var_cos2) / rowSums(var_cos2)
var_contrib

A matrix: 4 × 4 of type dbl

	Sepal.Length	Sepal.Width	Petal.Length	Petal.Width
PC1	13.060027	0.7144055	73.3884527	12.8371149
PC2	43.110881	53.3135721	3.0058080	0.5697384
PC3	33.875875	35.7497361	0.5811939	29.7931952
PC4	9.953217	10.2222863	23.0245453	56.7999515

var_contrib %>% 
as.data.frame() %>%
rownames_to_column('pc') %>%
pivot_longer(names_to = 'var', values_to = 'contrib_percent', -pc) %>%
ggplot(aes(y=var, x=contrib_percent)) + geom_col() + facet_wrap(~pc)

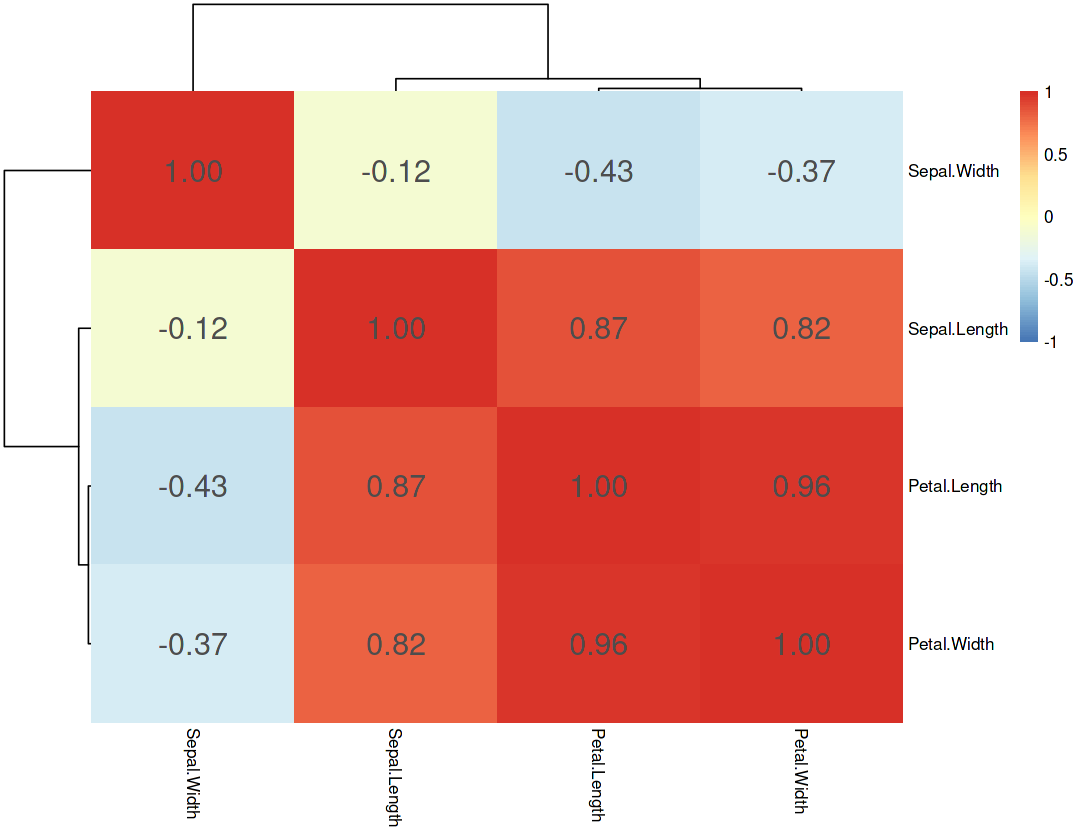
Correlation of all variables

Compare the correlations with the components loadings found by PCA

cor(iris.data) %>% 
pheatmap(display_numbers = TRUE, border_color = NA, fontsize_number = 18, breaks = seq(-1,1,length.out = 101))