PCA visualization in Python

import seaborn as sns
from sklearn import datasets
import pandas as pd
import numpy as np
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt

PCA visualization in Python#

This guide illustrates how to visualize the results of a PCA analysis

There is a sister notebook to this one in R here: PCA visualization in R

Dataset#

iris = datasets.load_iris()

# columns = variables
# rows = observations
iris.data[:5]

array([[5.1, 3.5, 1.4, 0.2],
       [4.9, 3. , 1.4, 0.2],
       [4.7, 3.2, 1.3, 0.2],
       [4.6, 3.1, 1.5, 0.2],
       [5. , 3.6, 1.4, 0.2]])

Run a PCA decomposition#

pca_res = PCA()
pca_x = pca_res.fit_transform(iris.data)
component_names = list(map(lambda i: 'PC'+str(i+1), range(pca_x.shape[1])))
pca_x.shape

(150, 4)

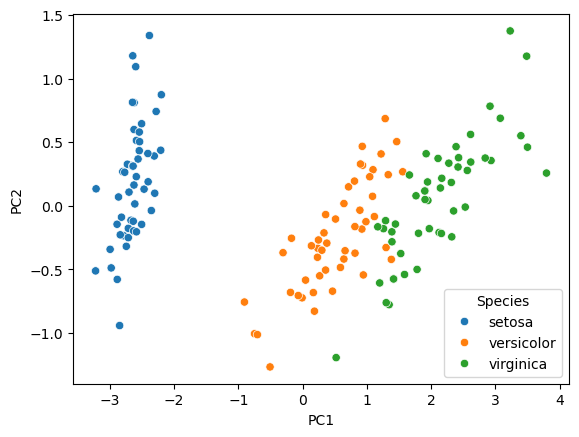
Scatter plot of observations#

Observations are projected on the first 2 components

species_names = list(map(lambda k: iris.target_names[k], iris.target))
df = pd.DataFrame(pca_x, columns=component_names)
df['Species'] = species_names
sns.scatterplot(data=df, x='PC1', y='PC2', hue='Species')
plt.show()
../../_images/de9e2201cef73c397362569e7534bba99acee8e9ac15880d9b54f181a2ea2e5b.png

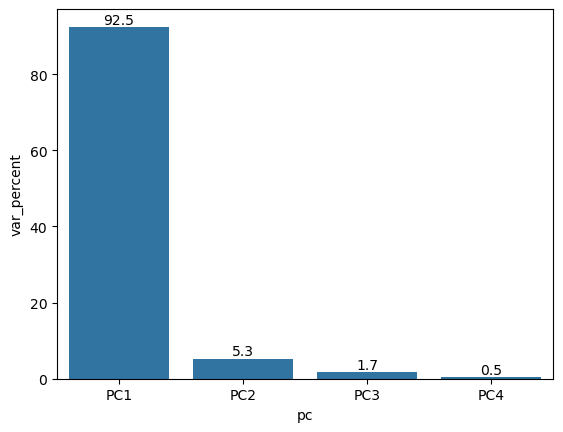
Explained variance (eigenvalues)#

The amount of variance explained by each of the components

pca_res.explained_variance_

array([4.22824171, 0.24267075, 0.0782095 , 0.02383509])

df = pd.DataFrame({'var_percent': 100*pca_res.explained_variance_ratio_, 'pc': component_names})
ax = sns.barplot(data=df, x='pc', y='var_percent')
ax.bar_label(ax.containers[0], fmt='%.1f')
plt.show()
../../_images/52f64fd03a1dc09c5e925d40376c767b5dc751ed72535dfc5639d07144799d5d.png

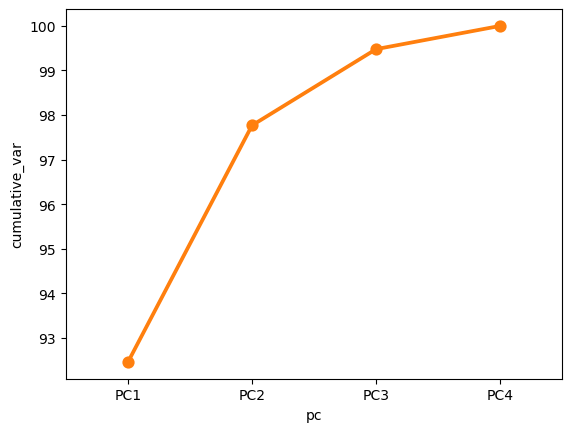
Cumulative variance#

df = pd.DataFrame({'var_percent': 100*pca_res.explained_variance_ratio_, 'pc': component_names})
df['cumulative_var'] = np.cumsum(df['var_percent'])
sns.lineplot(data=df, x='pc', y='cumulative_var')
sns.pointplot(data=df, x='pc', y='cumulative_var')
plt.show()
../../_images/57532575653cd4b0a5d32ffa8e4772aecdcd6481201f0148494ff3f58f4549d9.png

Component rotations (eigenvectors)#

Principal axes in feature space, representing the directions of maximum variance in the data

# columns = variables
# rows = components
pca_res.components_

array([[ 0.36138659, -0.08452251,  0.85667061,  0.3582892 ],
       [ 0.65658877,  0.73016143, -0.17337266, -0.07548102],
       [-0.58202985,  0.59791083,  0.07623608,  0.54583143],
       [ 0.31548719, -0.3197231 , -0.47983899,  0.75365743]])

df = pd.DataFrame(pca_res.components_, columns=iris.feature_names)
df['pc'] = component_names
df = df.melt(id_vars=['pc'])
sns.catplot(data=df, x='value', y='variable', col='pc', kind='bar', col_wrap=2, height=3)
plt.show()
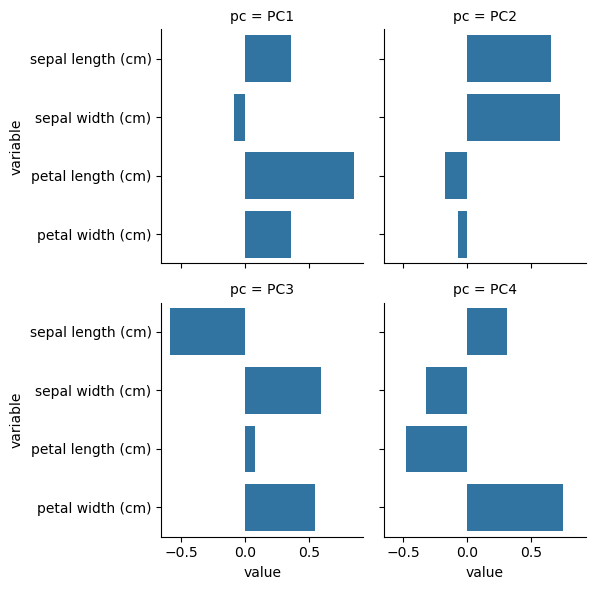
../../_images/a581d19dc40d9fdd7d37f494a676a35e743738b53d0e4ef7470be729eadd1758.png

Component loadings#

Eigenvectors scaled by the square root of the eigenvalues

sdev = np.sqrt(pca_res.explained_variance_)
var_cor = pca_res.components_.T * sdev

# columns = components
# rows = variables
var_cor

array([[ 0.743108  ,  0.32344628, -0.16277024,  0.04870686],
       [-0.17380102,  0.35968937,  0.16721151, -0.04936083],
       [ 1.76154511, -0.08540619,  0.02132015, -0.07408051],
       [ 0.73673893, -0.03718318,  0.15264701,  0.11635429]])

plt.figure(figsize=(8,6))

for i, r in enumerate(var_cor):
    plt.arrow(0, 0, r[0], r[1],head_width=0.03, head_length=0.03, color='black')
    plt.text(r[0] * 1.15, r[1] * 1.15, iris.feature_names[i], fontsize=10)

plt.axvline(x=0, linestyle='--', color='gray')
plt.axhline(y=0, linestyle='--', color='gray')
plt.xlabel('PC1', fontsize=10)
plt.ylabel('PC2', fontsize=10)
plt.show()
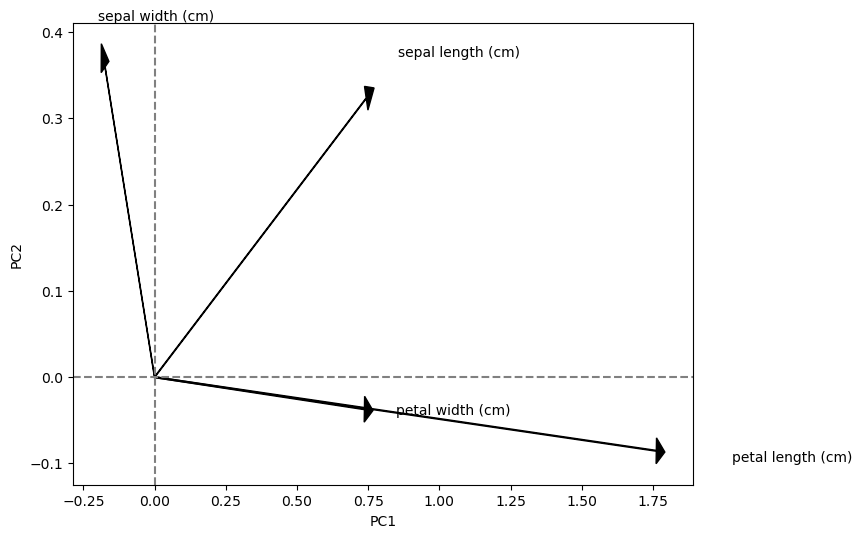
../../_images/a66555ed45e17ab546972fc9799e681ae585ea5df90d4165cac8f6804dd4f3ec.png

Component contributions#

Measures the contribution of the variables to each component

var_cos2 = var_cor ** 2
var_contrib = (100 * var_cos2) / var_cos2.sum(axis=0)

# columns = components
# rows = variables
var_contrib

array([[13.06002687, 43.11088146, 33.87587478,  9.95321689],
       [ 0.71440554, 53.31357208, 35.74973608, 10.2222863 ],
       [73.38845271,  3.00580802,  0.58119393, 23.02454534],
       [12.83711488,  0.56973844, 29.79319522, 56.79995147]])

df = pd.DataFrame(var_contrib.T, columns=iris.feature_names)
df['pc'] = component_names
df = df.melt(id_vars=['pc'], value_name='contrib_percent')
sns.catplot(data=df, x='contrib_percent', y='variable', col='pc', kind='bar', col_wrap=2, height=3)
plt.show()
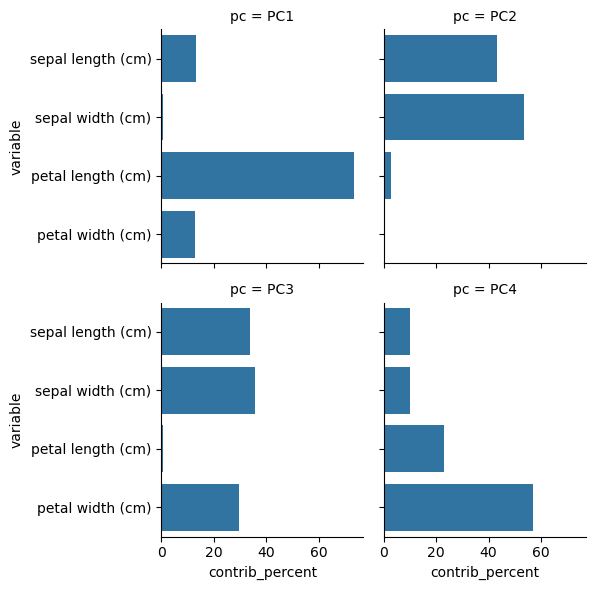
../../_images/529ebe494ee773d5a0cf74cb214fa22084944df993679510ca4faef06fbd0bf0.png

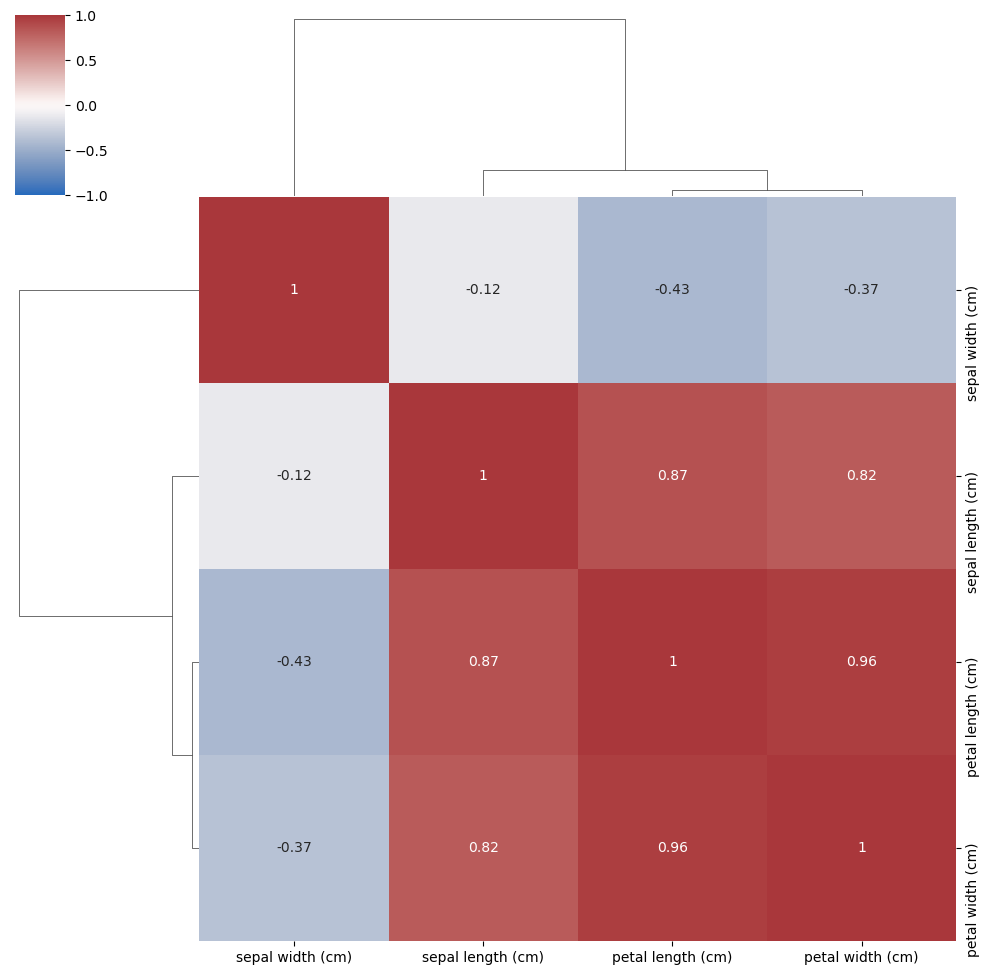
Correlation of all variables#

Compare the correlations with the components found by PCA

corr = np.corrcoef(iris.data.T)
sns.clustermap(corr, vmin=-1, vmax=1, cmap='vlag', annot=True, xticklabels=iris.feature_names, yticklabels=iris.feature_names)
plt.show()
../../_images/e5144435a0d7a5215e6537dcf92c9790ec80ec95a16bda254738cb7275a4615e.png
Contents